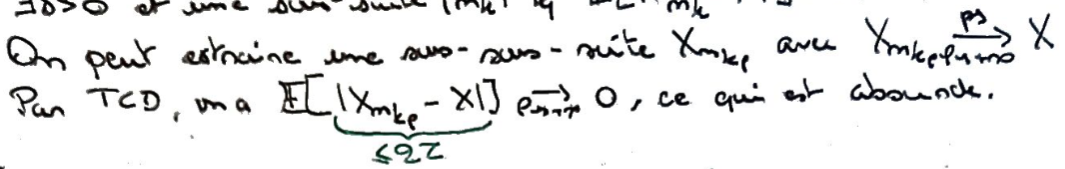Théorème de convergence dominée

Formulaire de report

Problème d'affichage Contenu de la note peu pertinent

• hypothèses :
    
• \((f_n)_n\) est une suite de fonctions mesurables qui converge pp vers \(f\)
    
• \(f\) est mesurable
    
• il existe \(g\) intégrable tq \(\forall n\geqslant0,\lvert f_n\rvert\overset{pp}\leqslant g\)
• résultats :
    
• \(f\) est intégrable
    
• $$\int f\,d\mu=\underset{n\to+\infty}{\operatorname{lim} }\int f_n\,d\mu$$
• éléments de preuve : lemme de Fatou

Questions de cours

Montrer que dans les hypothèses du théorème de convergence dominée, on peut remplacer la convergence presque-sûre par une convergence en probabilité.

Supposons par l'absurde qu'on ait une convergence en probabilités, mais pas le résultat du théorème.

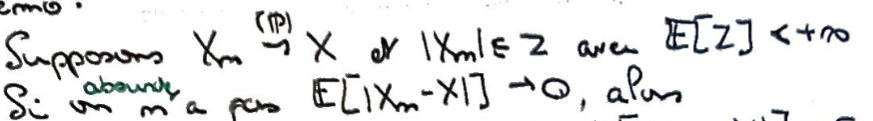
On peut alors extraire une sous-suite qui converge presque-sûrement, ce qui est absurde.